노력과 삽질 퇴적물

혼잣말처럼 넘기는 자료구조 (파트3) 본문

프로그래밍note/CS 기초

혼잣말처럼 넘기는 자료구조 (파트3)

MTG 2024. 1. 31. 16:50

 

목차
 기본 용어 및 개념
> 추상화, 성능 등등.
 배열
 스택
 큐
 연결 리스트
> 기본 개념
> 단순 연결 리스트
> 단순 원형 연결 리스트
> 이중 연결 리스트
 이진 트리
> 기본 개념
> 형태
> 연산
 그래프
> 기본 개념
> 기술하기
> 탐색
> 최소 신장 트리: 프림, 크루스컬, 솔린
 힙
> 기본 개념
> 형태
> 연산
 선택 트리
> 승자 트리, 패자 트리
 숲
 BS 트리
> 탐색, 삽입, 삭제
 BS변형
> Splay, AVL, BB
 멀티웨이 탐색 트리 ①
> m원, B, B*, B+
 멀티웨이 탐색 트리 ②
> 2-3 트리, 2-3-4 트리, 레드 블랙 트리
 마치며.

 

* 참조 서적중 초판이 1994년 이고 2020년 이후에도 개정판이 나온거 같은데 그걸로 봐도 되지 않을까 싶지만 제가 가지고 있던건 구판이다보니 이걸 기준으로
* 자체적으로 만들어둔 예제 코드는 C++(11)과 JAVA기준이며 C++의 경우 C++11과 C++14에서 구동 테스트 마친 코드입니다.
 
 
 
 
 
1. 그래프


1) 기본개념

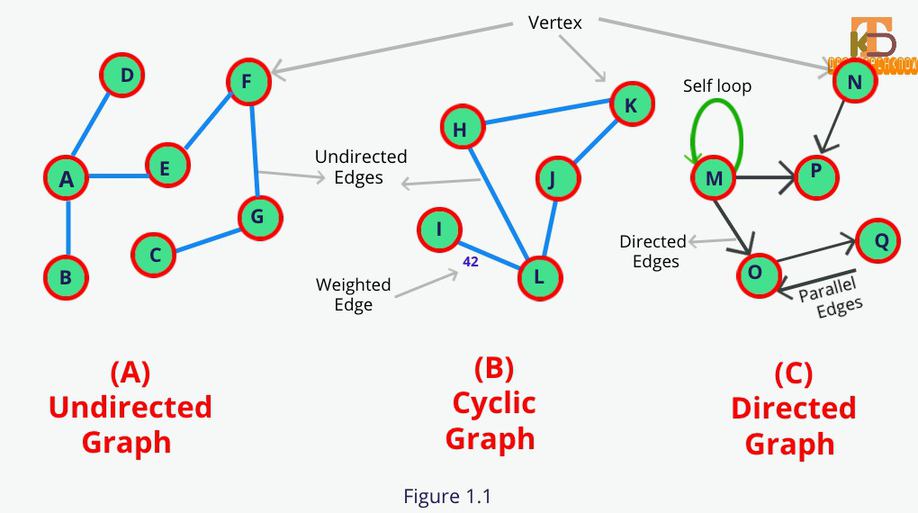
 정점(Vertex)  그래프상의 노드를 정점이라 한다.
 간선(Edge)  그래프의 노드를 연결하는 선.
 무방향 그래프
 (Undirected Graph)		  간선에 화살표로 방향 O = 방향성을 갖는무방향 그래프.
 무방향 그래프에서 간선 표기법 (V1, V2)
 방향 그래프
 (Directed Graph)		  간선에 화살표로 방향 X = 방향성이 없는 방향 그래프.
 방향 그래프에서 간선 표기법  {V1, V2}
 혼합 그래프  화살표이 있는 간선과 화살표가 없는 간선이 다 있는 그래프.
 다중 그래프  정점 사이의 간선이 2개 이상인 경우가 존재하는 그래프.
 가중 그래프
 (Weighted Graph)		  연결된 간선에 가중치(일종의 비용, 이동시간 등등)가 표기된 그래프로 방향 그래프와 가중 그래프를 합친 경우는 '네트워크'라 표현하기도 한다.
 희소 그래프
 (Sparse Graph)		  정점의 갯수에 비해 적은 간선을 가진 그래프로 
 완전 그래프  그래프에 있는 정점이 n개인 경우,
 (무방향 그래프) 간선이 (n*(n-1))/2개 다 연결된 그래프.
 (방향 그래프)    간선이 (n*(n-1))  개 다 연결된 그래프.
 널 그래프  간선으로 연결된게 없는 정점을 독립정점이라 하며, 독립 정점만 존재하는 그래프.
-> 사실 그래프중 사이클이 없는 단순 그래프가 트리다. 루트는 있으나 계층개념도 있고, 정점간의 경로가 1개만 있는 구조.
 
 
2) 기술하기
-> 두 정점을 연결한 간선이 있으면 그 정점에 대해 인접한다고 표현한다. 그래프에서 인접한 정점을 이용해 표현하는데는 '인접 행렬'(Adjacency Matrix)과 '인접 리스트'(Adjacency List)가 있다.
 
 
3) 탐색
-> "그래프에서도 마찬가지로 각 정점들은 간선을 타고 중복없이 한 번씩 방문하는 방법이 필요하다. ...(중략)... 나무 구조와 달리 그래프에서는 방향성이 없기 때문에 순회 순서가 유일하지 않다."   (p.713, C로 배우는 알고리즘2, 1996)
 
3-1) 깊이 우선 탐색(DFS. Depth First Search)
ⓐ 입력을 위한 루트 정점(혹은 시작점이 될 노드)를 선택.
ⓑ 정점을 스택.push
ⓒ 스택.pop 1회
ⓓ 단계 ⓒ에서 제거된 정점과 직접 연결된 인접한 정점(들)을 차례대로 스택.push
    (단, 스택내에 이미 존재하는 정점이나 방문했던 정점이 안 들어가게.)
ⓔ (스택.leng==0)? 종료 : 단계 ⓒ부터 다시
->  '스택'의 특성을 활용해 구현해 구현.
 
3-2) 너비 우선 탐색(BFS. Breadth First Search)
-> 0레벨부터 최하위 레벨까지 각 레벨별 노드를 확인. '큐'의 특성을 활용해 구현. 나머지는 파트2의 '이진트리 3) 연산' 참조.
 
 
4) 최소 신장 트리(Minimal?Minimum? Spanning Tree. MST)
-> "프림 알고리즘, 크루스컬 알고리즘 및 솔린 알고리즘이 대표적인 신장 트리 만들기 알고리즘입니다. 단, 이 알고리즘들이 항상 최저 비용인 신장 트리를 구하는것을 보장하지는 않습니다."  (p.318, 자료구조, 2023)
-> /* 방송대 교재에서는 MST에 대해 Minimal이라 했지만, 영문권 자료와 다른 참조 자료들은 전부 Minimum이여서 학파 차이의 영역으로 봐야 하는건가 싶어집니다. */
-> 4-1과 4-2는 programiz.com 설명 기준으로 요약&정리했습니다.
 
4-1) 프림 알고리즘(Prim Algorithm)
ⓐ 가중 그래프에서 정점 하나를 T[]에 입력
ⓑ T[]에 속한 정점들에 연결된 최소 비용 간선중 신규 정점을 T에 넣되, 싸이클이 형성되지 않아야.
ⓒ (모든 정점을 방문했는가==true) ? 종료 : 단계ⓑ부터 다시
-> 연결된 정점 기준으로 간선을 추가.
-> 시간 복잡도: 인접행렬 검색으로 하면 O(n^2)이 되고, 인접리스트등으로 하면 logN급
 
4-2) 크루스컬 알고리즘(Kruskal Algorithm)
ⓐ 모든 간선을 비용기준으로 오름차순 정렬
ⓑ 단계 ⓐ에 나온 결과를 T에 넣되, 싸이클이 형성되지 않는것만 넣는다.
ⓒ 모든 정점이 연결되어 있는지 확인하다.
-> 비용순으로 정렬된 간선들을 하나씩 추가.
-> 결과는 거의 비슷한거 같은데, 알고리즘은 프림보다 간결하다로.
 
4-3) 솔린 알고리즘(Sollin Algorithm)
ⓐ 그래프의 간선은 제외하고, 정점으로만 구성된 숲(forest)을 만든다.
ⓑ ⓐ번에서 만든 숲 내의 트리들을 최소 비용을 갖는 간선으로 연결한다.
ⓒ 남은 간선이 없거나 완전한 트리가 생성될 때까지 ⓑ번을 반복한다.





2. 힙

1) 기본개념
-> "우선순위 큐는 운영체제 등이 작업의 순서를 관리할 때 사용하는 중요한 자료구조입니다. ...(중략)... 힙은 우선순위 큐의 한 종류입니다. 우선순위 큐는 작동 방법은 정의하였지만 그것을 어떻게 구현해야 하는지는 정해지지 않았습니다. 우선순위 큐를 트리로 구현한 게 바로 힙입니다."  (p.205, 자료구조, 2023)
-> "흔히들 우선순위 큐에 대해서 오해하는 점은 우선순위 큐가 어떤 구체적인 자료구조라고 생각하는 것이다. 우선순위 큐는 순위에 의해 순서가 유지되면 관리되는 자료 구조의 추상적인 개념이다."  (p.387, C로 배우는 알고리즘, 1994)
-> /* 우선순위에 대한 처리가 가능한 '큐'의 일종으로 어디서는 완전 이진트리(맨 아래 오른쪽만 약간 빈 상태) 응용판, 어디서는 정렬 알고리즘으로 분류. 분류는 필요에 의한 정리인거니 그냥 어떤 연산과 처리를 가지는지에나 집중을 */
 
 
2) 형태
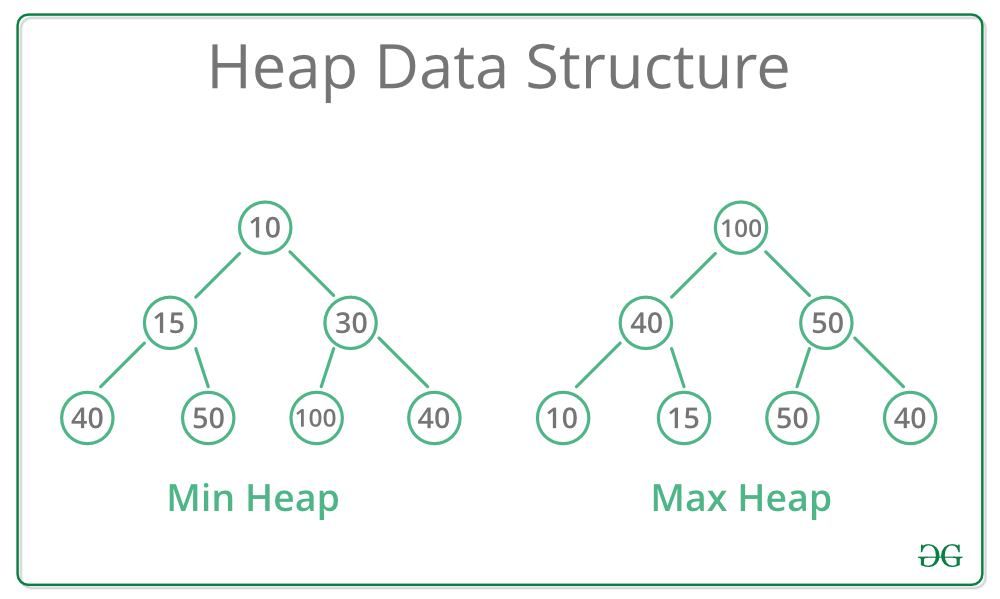
-> 루트의 노드값이 최소값이면 최소힙, 루트의 노드값이 최대값이면 최대힙이며 어느 힙인지에 따라 부모-자식 노드의 값에도 규칙이 정해진다. 단, 같은 부모를 둔 자식 노드간에는 정렬X.
-> 완전 이진트리이니 연결 리스트가 아닌 배열로 구현해도 메모리 낭비X. 배열로 구현시 루트노드는 arr[1]인것에 주의.
 
 
3) 연산
ⓐ insert. 힙에 데이터 삽입
ⓑ delete: 힙에서 루트노드 삭제
ⓒ peek: 힙에서 루트노드 데이터값 읽기
ⓓ isEmpty: 힙이 비었는지 확인
ⓔ size: 힙에 저장된 노드의 갯수 확인
 
 



기타. 참조자료

1) 서적
강태원, 정광식 저. 자료구조, 한국방송통신대학교출판문화원, 2023년.
이재규 저. C로 배우는 알고리즘, 세화, 1994년.
이재규 저. C로 배우는 알고리즘 2, 세화, 1996년.


2) 웹페이지
위키백과
> 프림 알고리즘 (접속: 2024-01-30)

geeksforgeeks
> Prim’s Algorithm for Minimum Spanning Tree (MST) (접속: 2024-01-30)
> Heap Data Structure (접속: 2024-01-31)
tutorialspoint.com
> Heap Data Structure (접속: 2024-01-31)
> Heap Sort Algorithm (접속: 2024-01-31)
programiz
> Graph Data Stucture  (접속: 2024-01-25)
> Prim's Algorithm (접속: 2024-01-30)
> Kruskal's Algorithm (접속: 2024-01-31)
> Heap Data Structure (접속: 2024-01-31)
> Heap Sort Algorithm (접속: 2024-01-31)


3) 블로그
개발자 강세영
> 최소 신장 트리와 관련 알고리즘 (접속: 2024-01-30)
falling_star3 (토끼는 개발개발) - velog
 




기타. 변경이력

일자
  변경이력
 2024-01-25  초안 작업 시작.
 2024-01-31  일반 공개. [#blogger] [#티스토리]

'프로그래밍note > CS 기초' 카테고리의 다른 글

혼잣말처럼 넘기는 자료구조 (파트4)  (0) 2024.03.15
혼잣말처럼 넘기는 자료구조 (파트2)  (0) 2024.01.24
2진수와 부동소수점 표현  (0) 2024.01.14
혼잣말처럼 넘기는 자료구조 (파트1)  (0) 2024.01.05
코딩도장 문제풀이  (0) 2015.03.10
'프로그래밍note/CS 기초' Related Articles more