노력과 삽질 퇴적물
혼잣말처럼 넘기는 자료구조 (파트2) 본문
|
목차
|
|
| 기본 용어 및 개념 > 추상화, 성능 등등. 배열 스택 큐 |
|
| 연결 리스트 > 기본 개념 > 단순 연결 리스트 > 단순 원형 연결 리스트 > 이중 연결 리스트 이진 트리 > 기본 개념 > 형태 > 연산 |
|
| 그래프 > 기본 개념 > 기술하기 > 탐색 > 최소 신장 트리: 프림, 크루스컬, 솔린 힙 > 기본 개념 > 형태 > 연산 |
|
| 선택 트리 > 승자 트리, 패자 트리 숲 BS 트리 > 탐색, 삽입, 삭제 BS변형 > Splay, AVL, BB 멀티웨이 탐색 트리 ① > m원, B, B*, B+ 멀티웨이 탐색 트리 ② > 2-3 트리, 2-3-4 트리, 레드 블랙 트리 마치며. |
|
* 참조 서적중 초판이 1994년 이고 2020년 이후에도 개정판이 나온거 같은데 그걸로 봐도 되지 않을까 싶지만 제가 가지고 있던건 구판이다보니 이걸 기준으로
* 자체적으로 만들어둔 예제 코드는 C++과 JAVA기준이며 C++의 경우 C++11과 C++14에서 구동 테스트 마친 코드입니다.
1. 연결 리스트
1) 기본 개념
-> "리스트의 원소들은 논리적인 순서만 따르면 되기 때문에 저장 위치를 연속적으로 메모리에 할당할 필요가 없습니다. 하지만 리스트의 원소들을 올바른 순서(논리적인 순서, 혹은 의미적인 순서를 유지하면서)에 따라 접근하기 위해서는 각 원소들 간의 순서를 표현해 줄 수 있는 프로그래밍 기법이 필요합니다." (p.88, 자료구조, 2023)
-> "연결 리스트가 배열과 다른 점은 배열은 메모리의 연속된 공간을 차지하는데 비해서 연결 리스트는 동적으로 수시로 할당 해체되기 때문에 메모리의 연속된 공간을 차지하지 못 한다. 그래서 연결 리스트의 각 요소들은 흩어져 있고 순서도 제대로 되어 있지 않다. 이런 연결 리스트의 순서를 유지시켜 주는 것은 링크(link)에 의해서 가능해진다." (p.124, C로 배우는 알고리즘, 1994)
-> /* 배열은 아파트처럼 논리적 순서=물리적 순서지만, 리스트는 논리적인 순서만 있어서 메모리상 모여있지는 않다. 가령 펜션에 휴가를 갔는데, 옆 건물이 바로 다음 호수가 아니라 한참 전 지난 곳이 다음 호수인 방식.
사족으로 배열로도 리스트 구현은 가능하지만, 길이의 변동이 잦을 경우 낮아지는 효율상 아무래도;;; */
2) 단순 연결 리스트(Simple Linked List or Singly Linked List)
| * 노드와 생성 | |
| C++ | JAVA |
| class SinglyNode { public: int mData; SinglyNode *mNext; }; class SingleLinkedList { public: SinglyNode *mHead;//머리 혹은 헤드 int mLength;//선택사항. SinglyLinkedList(): mHead(NULL), mLength(0) { } }; |
public class SinglyNode {//노드 구조 정의. 자바는 1클래스 in 1파일 public int mData; public SinglyNode mNext; } public class SinglyLinkedList { public SinglyNode mHead;//머리 혹은 헤드 public int mLength;//선택사항. public SinglyLinkedList() { mHead = null; mLength = 0; } } |
| -> 코드를 가장 간단한 형태로 뽑아내고자 멤버 변수를 public으로 했습니다. 실전에서는 getter/setter함수라던가 자바에서는 롬북&어노테이션으로 -> 생성자에서 멤버변수를 초기화하는건 연결 리스트 생성 함수를 대체하는 용도. |
|
| * 노드 삽입 | |
| C++ | JAVA |
| class SinglyLinkedList { public: ... ... ... void addEndNode(int argData) {//리스트 맨 끝에 삽입. SinglyNode* newNode = new SinglyNode(); newNode->mData = argData; newNode->mNext = nullptr; mLength+=1;//선택사항. if(this->mHead==nullptr)// 중요구간(1) { this->mHead = newNode; return; } //중요구간(2) SinglyNode* tmpNode = this->mHead; while (tmpNode->mNext != nullptr) { tmpNode = tmpNode->mNext; } tmpNode->mNext = newNode; } void insertNode(int argTargetData, int argNewData) {//특정 데이터값 노드뒤에 신규 노드 삽입. SinglyNode* prevNode = findNode(argTargetData); SinglyNode* newNode = new SinglyNode(); newNode->mData = argNewData; newNode->mNext = prevNode->mNext; prevNode->mNext = newNode; mLength+=1; } }; |
public class SingleLinkedList { ... ... ... public void addEndNode(int argData) {//리스트 맨 끝에 삽입. SingleNode newNode = new SingleNode(); newNode.mData = argData; newNode.mNext = null; if(this.mHead==null)// 중요구간(1) { this.mHead = newNode; mLength+=1; return; } //중요구간(2) SingleNode tmpNode = this.mHead; while(tmpNode.mNext !=null) { tmpNode = tmpNode.mNext; } tmpNode.mNext = newNode; mLength+=1; } void insertNode(int argTargetData, int argNewData) {//특정 데이터값 노드뒤에 신규 노드 삽입. SingleNode prevNode = findNode(argTargetData); SingleNode newNode = new SingleNode(); newNode.mData = argNewData; newNode.mNext = prevNode.mNext; prevNode.mNext = newNode; mLength+=1; } } |
| -> 중요구간(1): 연결 리스트 객체 생성후, 헤드가 없는 상태여서 (리스트)mHead에 새 노드를 그냥 넣어줌. -> 중요구간(2): 머리부터 시작해서 꼬리까지 찾아감. mHead를 tmpNode로 얕은 복사를 한터라 tmpNode의 mNext에 신규 노드 입력시, (리스트)mHead에도 즉시 반영됨. -> addEndNode: 공백인 리스트에 최초의 노드 입력을 하고 마치거나, 헤드의 후행의 후행의 (중략) 후행이 null이면 그 노드의 후행에 신규 노드 입력 -> insertNode: 특정 데이터를 가진 노드 뒤에 신규 노드 삽입.(중복되는 데이터가 없다는 전제하에) -> findNode함수는 이어지는 내용에 마저. |
|
| * 노드 검색 | |
| C++ | JAVA |
| class SingleLinkedList { public: ... ... ... SingleNode* findNode(int argTargetData) { SingleNode* result = this->mHead; while(result != null) { if(result->mData==argTargetData) {//CASE. 탐색 성공 및 완료 break; } result = result->mNext; } return result; } }; |
public class SingleLinkedList { ... ... ... public SingleNode findNode(int argTargetData) { SingleNode result = this.mHead; while(result != null) { if(result.mData==argTargetData) {//CASE. 탐색 성공 및 완료 break; } result = result.mNext; } return result; } } |
| -> 최소한 헤드에 해당되는 노드가 존재한다는 전제조건인 코드여서 만약 최초 입력없이도 사용이 가능하려면, 헤드가 비어있는지를 확인하고서 처리되는 예외처리가 함수 초반에 있어야 함. -> 필수사항이 아닌 mLength를 이용해서 반복문 횟수를 제어하면 연결 리스트상 몇 번째 노드를 탐색하는 방식도 가능. 상대적인 순번은 고정되어 있으니깐. -> while문에서 보이다시피, 항상 첫노드부터 순차적으로 탐색해야함.(단방향 링크) |
|
| * 노드 삭제 | |
| C++ | JAVA |
| class SingleLinkedList { public: ... ... ... int delNode(int argData) { int resultIdx = -1;//용도. 해당 노드의 순번값 boolean isExisted = false; SinglyNode* tmpNode = this->mHead; SinglyNode* prevNpde = tmpNode; while(tmpNode != nullptr) { resultIdx += 1; if(tmpNode->mData==argData) {//CASE. 탐색 성공 isExisted = true; prevNpde->mNext = tmpNode->mNext; delete tmpNode; tmpNode = nullptr; this->mLength-=1; break; } prevNpde = tmpNode; tmpNode = tmpNode->mNext; } if(isExisted==false){ resultIdx=-1; } return resultIdx; } }; |
public class SingleLinkedList { ... ... ... public int delNode(int argData) { int resultIdx = 0;//용도. 해당 노드의 순번값 boolean isExisted = false; SingleNode tmpNode = this.mHead; SingleNode prevNpde = tmpNode; while(tmpNode != null) { if(tmpNode.mData==argData) {//CASE. 탐색 성공 isExisted = true; prevNpde.mNext = tmpNode.mNext; tmpNode = null; mLength-=1; break; } prevNpde = tmpNode; tmpNode = tmpNode.mNext; resultIdx+=1; } if(isExisted==false){ resultIdx=-1; } return resultIdx; } } |
| -> '노드 검색' 응용으로 일치하는 노드를 찾았을때만 노드를 삭제한다. -> if(isDel==true) 블록내에서 삭제할 노드가 가진 다음 노드 정보를 prevNpde에게 인수인계 하고서 삭제처리. -> 함수의 반환값이 -1이면 일치하는 데이터를 가진 노드가 없는것이고, 0이상이면 해당되는 노드를 삭제했다는 표시로 구성. |
|
위의 기능들을 합쳐 브레이크 포인트를 통해 단계별로 테스트 가능합니다.
JAVA면 파일 확장자가 java인 파일들로
C++이면 파일 확장자가 cpp과 h인 파일들입니다.
| 함수 호출 예시 | 브레이크 포인트(C++, VS2022) |
|
singlyList.addEndNode( 2024 );
singlyList.addEndNode( 1 );
singlyList.addEndNode( 10 );
singlyList.addEndNode( 15 );
singlyList.addEndNode( 42 );
|
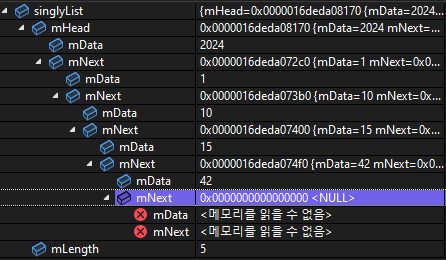 |
| singlyList.insertNode( 15, 30 ); -> 앞 단계와 비교시 기존 노드들의 주소값은 변동없이 data=30인 노드만 중간에 삽입. |
 |
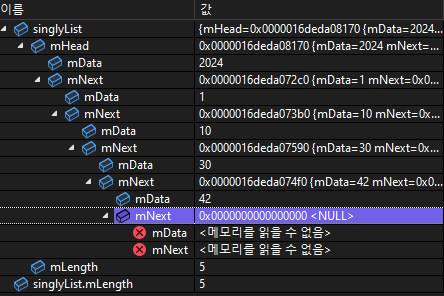
| singlyList.delNode( 15 ); -> 주소값을 보면, data=10인 노드의 mNext가 0x0000016deda07590로 data=30인 노드로 재연결. |
 |
3) 단순 원형 연결 리스트(Circular Linked List)
(*'원형 연결 리스트'의 응용이여서 세부적인 설명은 생략하고 코드만)
-> '단순 연결 리스트'에서 꼬리 노드의 mNext(혹은 링크)는 언제나 null이다. 이 꼬리의 mNext를 헤드 노드로 향하는지라 노드 탐색등의 루프에서도 차이가 있다. 벤젠 고리 설명에도 나오던 우로보로스처럼 헤드와 꼬리가 연결되어 순환이 가능하며 루프문의 종료도 아래와 같은 차이가 생긴다.
단순 연결 리스트 while (tmpNode->mNext != nullptr)단순 원형 연결 리스트 while (tempNode->mNext != this->mHead)
-> (중간 삽입이 아닌)신규 노드 삽입은 새로운 헤드 노드가 됨.
| 함수 호출 예시 | 브레이크 포인트(C++, VS2022) |
|
circularlyList.addEndNode(2024 );
circularlyList.addEndNode(1);
circularlyList.addEndNode(10);
circularlyList.addEndNode(15);
circularlyList.addEndNode(42);
|
 |
| circularlyList.insertNode(15, 30); -> 앞 단계와 비교시 기존 노드들의 주소값은 변동없이 data=30인 노드만 중간에 삽입. |
 |
4) 이중 연결 리스트(Doubly Linked List)
-> "연결 리스트(혹은 단순 연결 리스트)는 특정 노드의 선행 노드를 찾거나 리스트 원소들의 역순 검색을 할 경우에 성능이 나빠지거나 복잡한 프로그램 코드를 만들어내는 경향이 있습니다. 그럼 이러한 문제점을 해결하기 위해서 제안된 이중 연결 리스틀 ...(중략)..."
(p.147, 자료구조, 2023)
-> "이중 연결 리스트는 다음의 노드를 가리키는 링크와 전의 노드를 가리키는 링크 두 가지를 가져서 바로 전의 노드에도 접근할 수 있다는것이 가장 큰 장점이다."
(p.144, C로 배우는 알고리즘, 1994)
-> /* 단순 연결 리스트는 연결된 노드 정보(예시의 mNext)가 하나인 단방향 링크여서 시작점 기준으로 후행노드에 대한 순차적인 검색이 한계. 이중 연결 리스트는 (순번상)앞뒤로 연결된 노드에 대한 정보를 사용하여 순차과 역순 검색이 가능하다. 노드에 연결 노드 정보가 하나 더 들어가니 단순 연결보다는 메모리 소모가 좀더 있고, 노드 삽입/삭제시 절차가 좀더 있는 불가피한 단점. */
2. 이진 트리(Binary Tree, BT)
1) 기본 개념
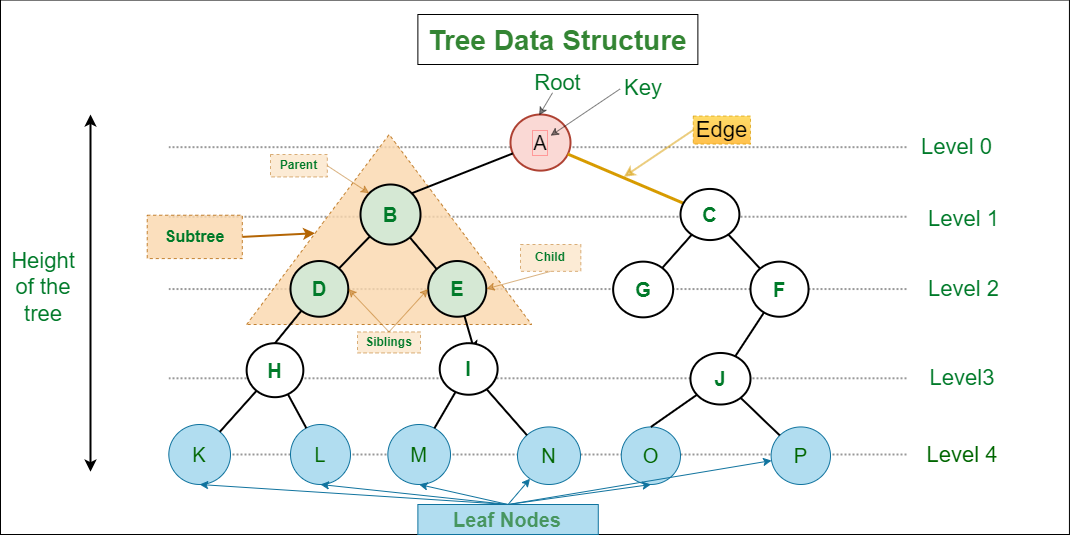
[그림. 자료구조 트리, 출처: geeksforgeeks.org]
-> 노드(node): 정점(vertex)로도 불리며, 트리내 구성원이다.
-> 루트 노드: 트리내 최상위 노드로 부모(노드)가 존재치 않으며, 현실의 족보로 치면 본관의 시조에 해당. 진입 차수(in degree)가 0인 노드라 표현하기도 한다.
-> 잎 노드: 트리내 최하위 노드로 자식(노드)가 존재치 않다. 현실로 치면 가계도상 내 밑으로 다음 항렬 세대가 없다.
-> 엣지(edge): 노드와 노드를 잇는 선.
-> 트리 레벨: 0레벨인 루트에서 최하단 노드까지 몇 단인지 세는것으로 0-base로 센다.
-> 트리 깊이: 깊이가 1인 루트에서 최하단 노드까지 몇 단인지 세는것으로 1-base로 센다.
-> 트리 크기: 트리내 노드의 갯수.
-> 진입 차수: 상위 노드에서 내려오는 엣지의 갯수. 루트(노드)만 0이고 나머지 노드는 1이다. (진입 차수가 2 이상이면 그래프)
-> 진출 차수: 하위 노드로 내려가는 엣지의 갯수. 잎(노드)만 0이고 나머지 노드는 1이나 2다.
2) 형태
| 정 이진 트리 | Full binary tree 모든 노드의 자식이 0아니면 2. -> 루트만 존재하는 트리와 포화 이진트리가 '정 이진 트리'에 포함. |
| 완전 이진 트리 | Complete binary tree k-1레벨까지 존재하는 트리기준으로 0~(k-2)레벨 노드들은 모두 자식이 있고, 최하층에서 맨 오른쪽만 덜 채워진 형태로 피라미드 그림에서 오른쪽 아래 귀퉁이 조각만 없는 모양새. |
| 포화 이진 트리 (or 가득찬 BT) |
Perfect binary tree k-1레벨까지 존재하는 트리에서 0~k-2레벨 노드들 진출 차수가 전부 2. -> 배열로 표현 가능 |
| 변질 트리 | Degenerate tree or Pathological tree 부모가 오직 하나의 자식만 가짐. -> 연결리스트처럼 동작. |
3) 연산
-> 배열로도 구현이 가능하나, 2^트리레벨 (k=0, 1, 2, ..., N)마다 나눠 각 레벨에 대응시키면 트리가 깊을수록 군데군데 자식 노드가 없으면 메모리 낭비 이슈가 존재해 보통 이중 연결 리스트로 구현.
-> 각 탐색별 예시는 다른 분 정리로 대체합니다. [#이진 트리 순회: 전위, 중위, 후위, 레벨]
-> 탐색종류
| 전위 순회 (Preorder traverse) |
재귀 호출 활용. preOrder(root) {//MEMO. 수도 코드 if(root==null){ return; } print(root.data); preOrder(root.left); preOrder(root.right); } |
| 중위 순회 (Onorder traverse) |
재귀 호출 활용. onOrder(root) {//MEMO. 수도 코드 if(root==null){ return; } onOrder(root.left); print(root.data); onOrder(root.right); } |
| 후위 순회 (Postorder traverse) |
재귀 호출 활용. postOrder(root) {//MEMO. 수도 코드 if(root==null){ return; } postOrder(root.left); postOrder(root.right); print(root.data); } |
| 너비 우선 탐색 (Breadth First Search. BFS) |
레벨 순회(Levelorder traverse)로도 불린다. (0레벨부터 N-1레벨까지)같은 레벨에 속하는 노드를 검사하고 다음 레벨로 넘어가서 반복한다. C++의 STL중 '큐'를 활용하면 비교적 쉽게 구현이 가능. /* 주로 그래프 파트에 나오곤 하지만, 예제 코드에서 순서대로 입력케 하는 기능이 필요하고, 트리하고 그래프는 겹치는 부분이 있어서 트리에 */ |
기타. 참조자료
1) 서적
강태원, 정광식 저. 자료구조, 한국방송통신대학교출판문화원, 2023년.
이재규 저. C로 배우는 알고리즘, 세화, 1994년.
2) 웹페이지
오픈튜토리얼스
> LinkedList - Java 구현 - Data Structure (자료구조) (접속: 2024-01-05)
위키백과
위키백과
> 이진 트리 (접속: 2024-01-17)
geeksforgeeks
> Introduction to Tree - Data Structure and Algorithm Tutorials (접속: 2024-01-15)
tutorialspoint.com
> Linked List Data Structure (접속: 2024-01-05)
programiz
> Types of Linked List - Singly linked, doubly linked and circular (접속: 2024-01-05)
3) 블로그
walbatrossw/java-data-structures: 자바 자료구조 구현 및 요약정리
> ch02-linked-list (접속: 2024-01-05)
(TIL) C++ 연결 리스트 - 강현길의 개발 성장기 블로그 (접속: 2024-01-05)
jiwon.me - Jiwon Park's Blog
> 이진 트리 순회: 전위, 중위, 후위, 레벨 (접속: 2024-01-19)
4) 기타
4) 기타
유튜브
> 19. C++ 클래스 객체로 singly linked list 구현, SLL SLL by class object - YouTube
> Circular Linked List | Insert, Delete, Complexity Analysis - YouTube
기타. 변경이력
|
일자
|
변경이력 |
| 2024-01-05 | 초안 작업 시작. |
| 2024-01-24 | 일반 공개. [#blogger] [#티스토리] |
'📂기초 및 세팅 note > CS 기초' 카테고리의 다른 글
| 혼잣말처럼 넘기는 자료구조 (파트4) (0) | 2024.03.15 |
|---|---|
| 혼잣말처럼 넘기는 자료구조 (파트3) (0) | 2024.01.31 |
| 2진수와 부동소수점 표현 (0) | 2024.01.14 |
| 혼잣말처럼 넘기는 자료구조 (파트1) (0) | 2024.01.05 |
| 코딩도장 문제풀이 (0) | 2015.03.10 |