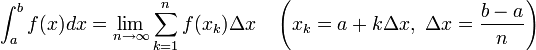노력과 삽질 퇴적물
게임 수학&물리 (1) 본문
해당 포스팅은 '까먹은거 다시 하기'가 목적이며 아래의 목차내에서만 다루겠습니다.
포스팅상 다루지 못하는 파트의 경우,
구현상 필요할때마다 찾아서 쓰는게 효율적이라 생각되어 생략했습니다.
수학 |
물리 |
1. 방정식: 1, 2, 3차 2. 직선 3. 원&구 4. 선형대수 > 행렬&행렬식&역행렬 > 벡터 5. 미적분 > 삼각함수 미분 > 적분, 적분을 이용한 넓이와 부피 | 1. 속도와 가속도 2. 운동의 법칙 3. 운동량과 충격량 4. 일과 에너지 * 포물선은 내용상 물리에서 종합적으로 정리 |
1. 방정식
1) 1차 방정식
Ax+B=0 [A!=0]
> 직선
> (A/B)x=0으로 기울기 구하는데 쓰임. [이하, 기울기 M]
> 두 직선이 직교(수직으로 겹치는거)할 경우, 두 직선의 M을 곱했을때 -1
예. (B/A) * (-A/B) = -1
2) 2차 방정식
Ax^2+Bx+C=0 [A!=0]
① 근의 공식 만들기
상수를 우변으로 넘긴후,
좌변에서 2차의 상수를 없애고,
좌변을 완전제곱으로 만듭니다.
제곱을 ^(1/2)시켰기 때문에 우변에 ±가 붙습니다.
짝수 공식의 경우, [B=2k]등으로 대입시키면 공식의 표현이 좀더 간결해집니다.
② 근을 이용한 계수의 관계
x의 근이 α와 β로 정의시,
③ 2차 함수 그래프
예: (X+1)(X-2) |
Ax^2+Bx+C는 포물선형 그래프가 된다. > A>0, 포물선이 아래로 막힘.(=최소값 존재) > A<0, 포물선이 위로 막힘.(=최대값 존재) -> 연상법. 바닥이 둥근 컵에 물을 채우는데, 물을 담으면(+) 컵을 세운거고, 물을 쏟으면(-) 컵을 엎은것. 근의 갯수만큼 X축과 겹친다. > 2개: (x+α)(x+β) B^2 - 4AC > 0 > 1개: Ax(x+α) B^2 - 4AC = 0 > 0개: Ax^2+C B^2 - 4AC < 0 * 그래프 툴 #PAGE |
3) 3차 방정식
Ax^3+Bx^2+Cx+D=0 [A!=0]
① 3차 함수 그래프
X축과 접하는 갯수 == 근의 갯수 |
4) 활용, 충돌체크
-> 두 직선이 만나는가?
Ax+B=0, A'x+B'=0
Ax+B = A'x+B'
(A-A')x = B'-B
2. 직선
1) 점과 직선
① 두 점 사이의 거리
-> A(x1, y1), B(x2, y2)
{ (x1-x2)^2+(y1-y2)^2 }^(1/2)
1 2 3 4 5 6 7 8 | import math; def PrintDistance(pt_a, pt_b): result = math.sqrt( math.pow(pt_a[0]-pt_b[0], 2) + math.pow(pt_a[1]-pt_b[1], 2) ); print result; pass; PrintDistance([20,16], [4, 9]); | cs |
② 두 직선 관계성
|
평행 |
일치 | 수직 |
표준형 y = mx + a // m이 기울기 y = m'x + b // m'이 기울기 |
m = m' a ≠ b |
m = m' a = b | m * m' = -1 |
일반형 ax+by+c=0 a'x+b'y+d=0 |
a/a' = b/b' ≠ c/c' |
a/a' = b/b' = c/c' | a*a' + b*b' = 0 |
연립 방정식 근의 갯수 | X | ∞ | 1 |
> 수직이 되는 두 직선의 유형중, 접선과 법선도 있다.
2) 점과 직선 사이의 거리
-> 점과 평면의 경우, 해당 공식을 3차원으로 늘려서 사용하면 가능.
P(x1, y1) 직선 ax2+by2+c = 0 |
① 수선(점과 직선이 수직으로 만나는) 방정식 -> y - y1 = (x-x1) * {(y2-y1)/(x2-x1)} ② 직선과 교점의 좌표 ③ A와 B의 거리 |
1 2 3 4 5 6 7 8 9 10 11 12 13 | def PointToLine(pt_a, line): result = pt_a[0]*line[0] + pt_a[1]*line[1] + line[2];# aX+bY+c if result < 0: result *= -1; pass; result /= math.sqrt( math.pow(pt_a[0], 2) + math.pow(pt_a[1], 2) ); print result ; pass; PointToLine([0, -1], [3, -2, 1]);#example | cs |
3. 원&구
1) 원의 방정식
-> (평면기준) 중심점(a, b)에서 일정한 거리(반지름r)에 있는 점들의 연속.
① 표준형: (x-a)^2+(y-b)^2 = r^2
② 일반형: x^2+y^2+Ax+By+C = 0
2) 거리관계
① 두원의 위치관계 |
* 두 원의 반지름은 각각 r, r' [단, r>r'] / 원의 중심점사이의 거리=d d > r+r' 두 원은 접점이 전혀 없다. (충돌X) d = r+r' (접점이 1개인) 외접. r-r < d < r+r' 두 원의 접점이 2개. d = r-r' (접점이 1개인) 내접. //작은 원이 큰원 속에 포함. d < r-r' //작은원이 큰원 내부 |
|
② 공통 접선의 거리 |
* 원의 중심점사이의 거리=d 공통외접선 l: (d^2 - (r-r')^2)^(1/2) 공통내접선 l: (d^2 - (r+r')^2)^(1/2) |
|
③ 원과 접선 | * 원밖의 점(a,b) 접선의 방정식 y-b = m(x-a) | |
*활용
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 | #!/usr/bin/env python # -*- coding: utf-8 -*- import math; def GetCollision(circle1, circle2): distance = math.sqrt( math.pow(circle1[0]-circle2[0], 2) + math.pow(circle1[1]-circle2[1], 2) ); if circle1[2]<circle2[2]:#반지름 길이에 따른 추가처리 tmp = circle2[2]; circle2[2] = circle1[2]; circle1[2] = tmp; pass; if distance <= (circle1[2] - circle2[2]): print "It's a bullet hole. remove bullet"; pass; elif distance > (circle1[2] + circle2[2]): print "NOT Collision"; pass; elif distance==(circle1[2] + circle2[2]): print "light scratch"; pass; elif distance < (circle1[2] + circle2[2]): print "deep scratch"; pass; pass;# END. GetCollision GetCollision([0, 0, 2], [3, -4, 2]);#NOT Collision GetCollision([0, 0, 2], [3, -4, 3]);#light scratch GetCollision([0, 0, 2], [3, -4, 4]);#deep scratch GetCollision([0, 0, 2], [3, -4, 10]);#It's a bullet hole. remove bullet | cs |
3) 구의 방정식
① 표준형: (x-a)^2+(y-b)^2+(z-c)^2 = r^2
② 일반형: x^2+y^2+z^2 = r^2
4. 선형대수
1) 행렬
-> [#위키백과, 행렬]
① 행렬의 합/차 |
합하려는 행렬들의 규격이 일치해야 한다. 계산하려는 행렬의 순서를 바꿔도 계산에 지장X |
|
② 행렬의 곱 |
곱하려는 행렬들의 규격이 호환되어야 한다.(?) -> 2*4행렬과 4*3행렬 [O] 2*4행렬과 3*4행렬 [X] 계산하려는 행렬의 순서를 바꿔도 계산에 지장O |
|
③ 항등행렬 |
I로 표기되곤 한다. 왼쪽 위->오른쪽 아래방향 대각선의 행렬원이 1이고 나머지가 0인 행렬. |
|
④ 전치행렬[A^t] |
[#참조] -> (연상법)손바닥을 가로방향&엄지가y+방향일때 손바닥을 뒤집어 손등이 보이고 엄지가 x+방향이 되는 회전. |
|
2) 행렬식
① 행렬식의 성질
* 한 행에만 N배를 하면, 행렬식의 값도 N가 된다. [단, N차 정방행렬]
* 두행의 원소가 비례관계이면 행렬식은 0
* 특정행을 N배해서 다른행에 더해도 행렬식값이 변하지 않는다.
* |A| = |A 전치행렬|
* |A*B| = |B|*|A|
② 계산
-> '행렬을 인수분해' / '일반화된 N차 정방행렬'이 라는 표기로도 있다.
* 2차원 행렬 |
A = [[a, b], [c, d]] 일때, │A│ = Det(A) = ad-bc |
|
* 3차원(이상) 행렬 -> laplace전개 활용 |
A = [[a, b, c], [d, e, f], [g, h, i]] 일때, 2가지 방법으로 구할수 있으나 공식으로는 동일하다. Det(A) = a(ei-fh) - b(di-fg) + c(dh-eg) -> [#참조링크] |
|
3) 행렬 연산
-> [#참조, 가우스 소거법]
-> 행렬식 값이 0이면 역행렬은 존재X
-> [#참조, 역행렬의 성질]
① 2차원 행렬, 역행렬
-> 역대각선(우측상단에서 좌측하단)기준으로 뒤집고, 대각선 행렬원소는 *=-1
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 | #!/usr/bin/env python # -*- coding: utf-8 -*- import math; def InverseMatrix_2D(matrix): tmp = 1.0/(matrix[0][0]*matrix[1][1] - matrix[0][1]*matrix[1][0]); print tmp;#(1/행렬식의 값) if tmp==0: print "Inverse matrix isn't exist." return; pass; tmp2 = matrix[0][0]; matrix[0][0] = matrix[1][1]; matrix[1][1] = tmp2; matrix[0][1] *= -1; matrix[1][0] *= -1; for row in range(0, 2): for col in range(0, 2): matrix[row][col] *= tmp; pass; pass; print matrix; pass; matrix = [[30, 40], [-20, -10]]; InverseMatrix_2D(matrix); | cs |
② 3차원 행렬, 역행렬
-> 1/│A│ * adj(A)
-> [#계산법]
-> [#참조 링크]
③ 행렬의 계수
* 성질
-> 전치행렬화 해도 계수는 동일
-> 두행을 바꾸어도 동일한 계수
-> 특정행만 N배해도 계수는 동일 [단, N은 0이 아님]
-> 특정행을 N배해서 다른행에 더해도 계수는 동일
-> 0으로만 구성된 행은 추가/제거해도 계수는 동일
④ 1차 연립방정식과 계수
-> 행렬A와 B의 계수값에 따라 연립방정식 근의 갯수가 달라진다.
5) 벡터
① 벡터의 성질
-> [#참조링크]
② 연산
합 → → → AB + BC = AC |
* 3단 논법과 같은 흐름. A에서 B로 이동, B에서 C로 이동. 결론. A에서 C로 이동했다. |
|
차 → → → AC - AB = BC |
→ → → AC +(-AB) = BC //벡터는 방향과 크기를 나타내는거라서 → → → AC + BA = BC //벡터의 성질상 합&차는 순서를 바꿔도 계산에 지장X |
|
③ 벡터의 성분
평면벡터 → → a = (a1, a2), b = (b1, b2) |
→ AB = (b1-a1, b2-a2) //성분 → |AB| = {(b1-a1)^2 + (b2-a2)^2}^(1/2) //크기 |
|
공간벡터 → a = (a1, a2, a3) |
→ |a| = {a1^2 + a2^2 + a3^2}^(1/2) |
|
| 방향코사인 | [#참조링크] | |
④ 벡터의 내적
> 두 벡터의 내적은 스칼라다. (=크기값만 있다.)
평면벡터의 내적 | → → a · b = |a||b| * cosΘ //여기서 cos각은 | |
성분표시 → → a = (a1, a2), b = (b1, b2) 일때 | → → | |
| 내적의 성질 | 교환법칙 가능 분배법칙 가능 결합법칙 가능 | |
| 벡터의 수직 (영벡터가 아닌 두 벡터) | → → → → a ⊥ b, a · b = 0 // cos 90° == 0 | |
| 벡터의 평행 (영벡터가 아닌 두 벡터) | → → a = k * b | |
⑤ 벡터의 외적
> 방향과 크기를 동시에 가짐.
> 벡터 a&b로 이루어지는 평면에 수직하는 벡터가 나온다.
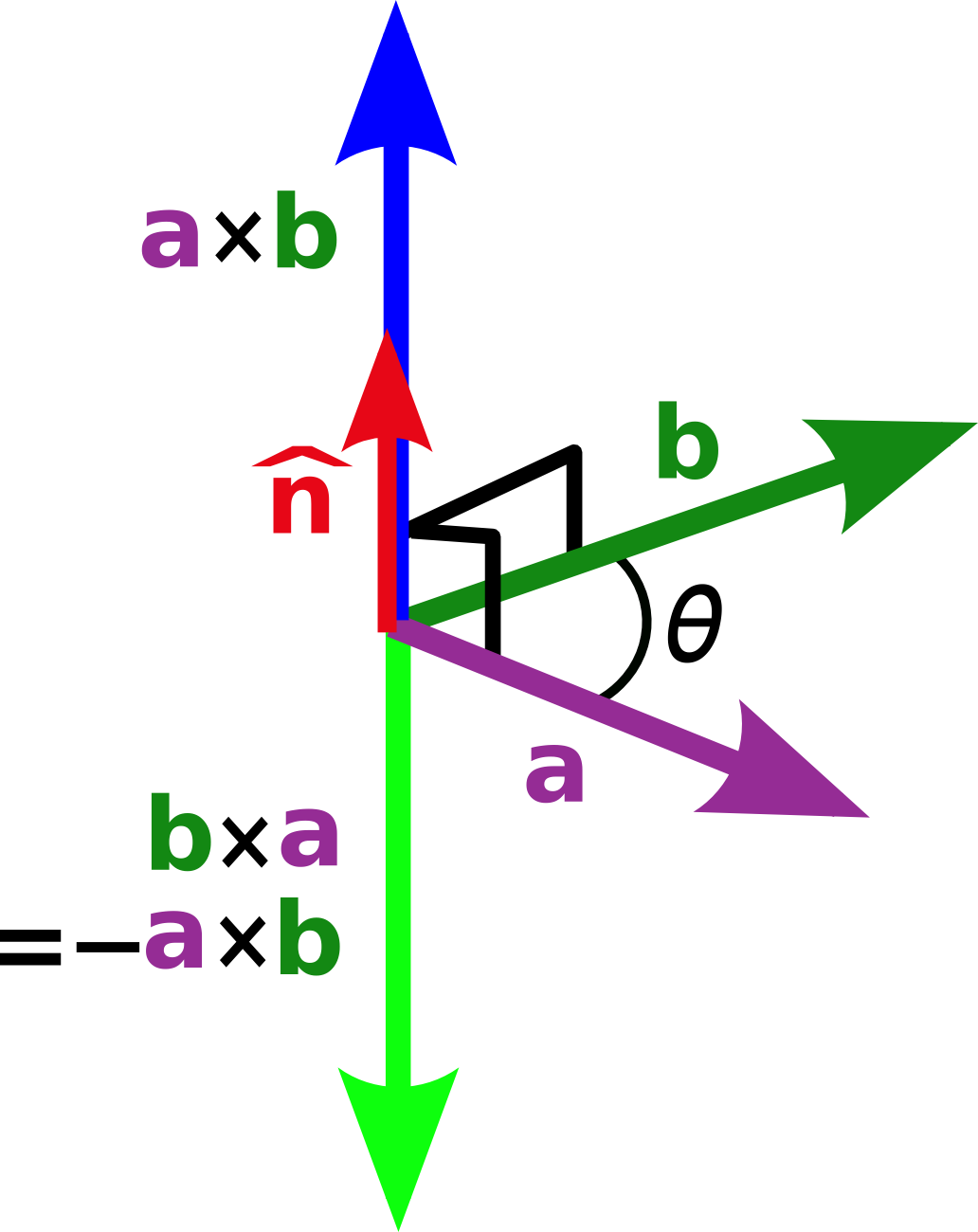
FAL, https://commons.wikimedia.org/w/index.php?curid=334210
평면벡터의 외적 | → → → → | |
| → → a = (a1, a2, a3), b = (b1, b2, b3) 일때, a x b => │ a1 a2 a3 │ │ b1 b2 b3│ │ x y z │ => (x y z) = (a2*b3-a3*b2, a1*b3-a3*b1, a1*b2-a2*b1) | ||
⑥ 기타
> 단위벡터: 크기가 1인 벡터, 방향만 계산할때 유용.
> 일반벡터(Normal Vector): [#참조링크]
5. 미적분
* 미분<->적분의 관계
> 구체를 일정한 칸으로 자르면 미분, 칸칸히 잘랐던 오브젝트를 다시 붙이면 적분.
1) 삼각함수
① 그래프
|
|
특수각 > sinΘ: 0°=0, 30°=1/2, 45°=√2/2, 60°=(√3)/2, 90°=1 > cosΘ: 0°=1, 30°=(√3)/2, 45°=√2/2, 60°=1/2, 90°=0 > tanΘ: 0°=1, 30°=1/(√3), 45°=1, 60°=√3, 90°=∞ * 상단의 그래프 기준으로 1/2π당 사분면 1 영역과 대응되므로 그에 맞춰 루프등을 시키면 계산 가능. | |
② 연산
덧셈정리 |
sin(α+β) = sinα*cosβ + sinβ*cosα sin(α-β) = sinα*cosβ - sinβ*cosα //[0, π]기준으로 각도가 클수록 값이 커서 con(α+β) = cosα*cosβ - sinα*sinβ con(α-β) = cosα*cosβ + sinαβ*sinβ //[0, π]기준으로 각도가 클수록 값이 작아서 tan(α+β) = (tanα+tanβ)/(1-tanαtanβ) tan(α-β) = (tanα-tanβ)/(1+tanαtanβ) |
|
삼각함수간 관계 |
tanΘ = (sinΘ)/conΘ (sinΘ)^2+(cosΘ)^2 = 1 1 + (tanΘ)^2 = (secΘ)^2 1 + (cotΘ)^2 = (cosecΘ)^2 |
|
배각의 공식 |
sin2α = 2sinα*cosβ cos2α = (cosα)^2 - (sinα)^2 = 2*(cosα)^2 - 1 = 1 - 2*(sinα)^2 tan2α = (2*tanα) / (1-(tanα)^2) sin3α = 3sinα - 4(sinα)^3 cos3α = 4*(cosα)^3 - 3*cosα tan3α = (3*tanα-(tanα)^3) / (1-3*(tanα)^2) |
|
그외. |
반각공식 [#참조링크] 곱<->합,차 변환 |
|
2) 미분종류별 미분공식
* 함수 f(x)에서 도함수 f'(x)를 구하는것을 함수를 x에 대하여 미분한다고 한다.
-> 도함수 f'(x) == y' == dy/dx == d/dx f(x)
① 기본 미분법 | ※ 다항함수 f(x) = c [c는 상수]이면, f'(x) = 0 {cf(x)}' = cf'(x) {f(x) ± g(x)}' = f'(x) ± g'(x) {f(x) * g(x)}' = f'(x)*g(x) + f(x)*g'(x) f(x) = (ax+b)^n [n은 자연수]일때, f'(x) = (ax+b)' * (ax+b)^(n-1) 분수 > y = f(x)/g(x) = f(x) * (g(x)^-1) y' = {f'(x)*(g(x)^-1) + -1 * f(x)g'(x)}*{g(x)}^2 = {f'(x)*(g(x)^-1) - * f(x)g'(x)}*{g(x)}^2 | |
② 삼각함수 | (sinΘ)' = cosΘ (cosΘ)' = -sinΘ (tanΘ)' = (secΘ)^2 = 1+(tanΘ)^2 (cosecΘ)' = (1/sinΘ)' = -(1/sinΘ)*cotΘ (secΘ)' = (1/cosΘ)' = secΘ * tanΘ (cotΘ)' = (1/tanΘ)' = -(cosecΘ)^2 [#참조링크, 삼각함수의 미분] | |
| ③ 로그함수&지수함수 | (ln x)' = 1/x [단, x>0] //로그 밑수가 e면 ln으로 표기 (logax)' = 1/(x * ln a) [밑수a>0, a!=1, x>0] -> 참고로 logax = log x/log a [밑수는 10으로 생략] -> logax = 1/logxa -> logax * logxc = logac {ln |f(x)|}' = f'(x) / f(x) (e^x)' = e^x (a^x)' = a^x * lna --> a^x [단, a>0] {e^f(x)}' = {e^f(x)} * f'(x) {a^f(x)}' = {a^f(x)} * lna * f'(x) | |
| ④ 편미분 | 함수에서 x나 y를 상수로 간주한채 미분한다. 예. -> f = ax^2 + bxy + cy^2일때, ∂/∂x f = 2ax + by + 0 ∂/∂y f = 0 + bx + 2cy | |
| ⑤ 그외 | N계도함수(or 고계도함수) > 함수를 N번 미분하는것이다. 예. y = ax^2 + bx + c y' = 2ax + b y'' = 2a //2계 도함수 | |
3) 미분과 활용
① 속도와 가속도
위치 x=f(t)일때
> (위치)' = 속도
> (속도)' = 가속도
② 함수관련
| 증가와 감수 | 증가함수 > f'(x) ≥ 0 > f'(x) > 0인 구간에서 증가함수 감소함수 > f'(x) ≤ 0 > f'(x) < 0인 구간에서 감소함수 | |
| 극대와 극소 | 극대/극소의 경우 f'(x) = 0인 값을 활용. | |
평균값의 정리 | ||
4) 적분
① 부정적분 | ∫f(x) dx = F(x) + c | |
② 정적분 |
미분된 함수 f(x)를 폐구간[a, b]를 기준으로 계산 F(b) - F(a) | |
③ 2중 적분 | 적분을 2중으로 계산하는것. | |
④ 활용법 | 넓이와 부피 | |
기타. 참조자료
게임 프로그래머를 위한 기초 수학 및 물리 - [#8장][#9장]
'📂게임개발 note > 미분류' 카테고리의 다른 글
| 현재 실무에서 주로 쓰는 개발툴들 (0) | 2022.07.30 |
|---|---|
| 신입 게임개발자, 포트폴리오에서 퇴사까지 (2) | 2018.05.07 |
| 시나리오: 소재구상 및 발굴용 자료 모음 (0) | 2014.08.17 |
| 플러그인, 신텍스 하이라이터 (0) | 2013.08.26 |
| SVN: TortoiseSVN 사용하기 (0) | 2013.08.02 |